По оси ординат обычно откладываются расчетные значения, а по оси абсцисс - наблюденные. Можно и наоборот, принципиальной разницы нет, но тому, кто привык «читать» этот график каким-либо одним образом, порою бывает сложно переключиться на другой. Умение бегло читать этот график, т.е. с одного взгляда на него, увидеть чего не хватает в модели — важнейший навык гидрогеолога-модельера. Попробую объяснить азы этой премудрости с помощью наглядных примеров (картинки все кликабельны).
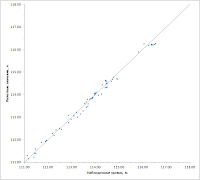
Очевидно, что чем ближе точки к диагонали, тем меньше разница между наблюденными и расчетными значениями и тем качественнее решена обратная задача. На рисунке показана практически идеально решенная задача. Скажу по секрету — ее пришлось придумывать, в реальности такого почти никогда не бывает и если вы, паче чаяния, являетесь экспертом, то знайте, что такой график — повод заподозрить модель в фиктивности. Впрочем, тут не все так просто — крайне важно не забывать про масштаб графика. С виду идеальный диагональный график может на поверку таить в себе невязку в десятки метров.
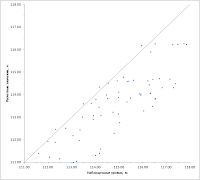
Два типичных графика: расчетные значения все дружно оказались выше или ниже наблюденных. В первом случае вы затопили, а во втором — пересушили модель. Если вы думаете, что я подскажу, как с этим бороться, то вы ошибаетесь. Увы, универсального рецепта не существует — все слишком сильно зависит от схематизации модели. Где-то надо поиграться с расходами на питающих границах, где-то менять фильтрационные параметры (характерно для многослойных толщ, в которых активно развито вертикальное перетекание — они бывают очень чувствительны к проницаемости разделяющих слоев), а где-то и вовсе придется пересматривать всю схематизацию. Ну, это если у вас вдруг настолько полные исходные данные, что ни фильтрационных свойств не изменишь, ни расходных характеристик, но это тоже больше из области ненаучной фантастики.
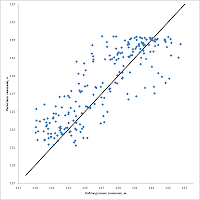
Еще один типичный вид диагонального графика — диагональ проходит через «облако» точек. Его особенность заключается в том, что в зависимости от характера исходных данных, он может как подтверждать достаточное качество решения обратной задачи, так и говорить об обратном. Удивительно, но объясняется просто. Если вы имеете дело с большим набором разновременных замеров уровня подземных вод (типичная ситуация при работе фондовыми данными), то совершенно невозможно «уложить все точки на диагональ» — просто потому, что для каждого замера характерны свои отличные от остальных граничные условия. Грубо говоря, часть замеров может быть сделано в зимнюю межень и характеризоваться уровнем заметно ниже среднегодичного, а часть - в весенний паводок, с уровнем выше среднегодичного. Пытаясь угодить и тем и этим вы получите либо страшно ошибочную модель, либо вообще ничего не добьетесь, только нервы потратите. Поэтому в данном случае обратную задачу можно считать решенной удовлетворительно, важно лишь следить за тем, чтоб разница между наблюденными и расчетными значениями не вылетала за амплитуду колебаний уровня подземных вод. А если делать все совсем по-уму, то надо на графике «меженные» и «паводковые» скважины рисовать разным цветом и следить, чтоб нужный цвет был с нужной стороны от диагонали.
Теперь совершенно очевидно, когда такой график будет говорить нам, что что-то мы напортачили в схематизации: когда вся масса замеров была проведена за относительно короткий промежуток времени, в течение которого не случалось резких изменений климатической обстановки. Кстати, из этого графика тоже понятно, что мы накосячили, но не совсем понятно — в чем.
Численным критерием качества решения обратной задачи традиционно является средний квадрат ошибки (Mean squared error, в PMWin он почему-то назван Variance), о котором я расскажу в следующий раз.