Гидрогеологический дайджест

• Water Pollution. Сборник статей на тему загрязнения воды.
• GB3D — 3D geological model for Great Britain. Британцы просто монстры какие-то. Обратите внимание на общедоступную базу колонок разведочных скважин. Жутко завидую.

Москва-река - карта фарватера, глубин, портов, шлюзов

Очень полезную для нашего брата карту выложили на сайте etomesto.ru: Москва-река - карта фарватера, глубин, портов, шлюзов.

Гидрогеологический форум

Внимательные читатели блога наверное заметили, что я открыл новую рубрику: гидрогеологический форум. Прошу всех, присоединяйтесь и давайте решать наши проблемы и вопросы вместе. Я знаю, среди моих читателей есть замечательные специалисты в самых разных областях гидрогеологии и смежных наук. Уверен, нам есть что обсудить.
Форум работает на движке Google Groups, так что если кому удобнее — присоединяйтесь там: Google группа Гидрогеология

Диагональный график

При калибровке модели основным критерием качества решения обратной задачи является степень совпадения модельных и натурных уровней в скважинах. В графическом виде это сравнение принято показывать в виде т.н. диагонального графика.
По оси ординат обычно откладываются расчетные значения, а по оси абсцисс - наблюденные. Можно и наоборот, принципиальной разницы нет, но тому, кто привык «читать» этот график каким-либо одним образом, порою бывает сложно переключиться на другой. Умение бегло читать этот график, т.е. с одного взгляда на него, увидеть чего не хватает в модели — важнейший навык гидрогеолога-модельера. Попробую объяснить азы этой премудрости с помощью наглядных примеров (картинки все кликабельны).

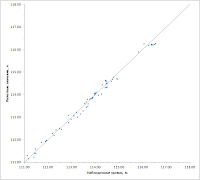
Очевидно, что чем ближе точки к диагонали, тем меньше разница между наблюденными и расчетными значениями и тем качественнее решена обратная задача. На рисунке показана практически идеально решенная задача. Скажу по секрету — ее пришлось придумывать, в реальности такого почти никогда не бывает и если вы, паче чаяния, являетесь экспертом, то знайте, что такой график — повод заподозрить модель в фиктивности. Впрочем, тут не все так просто — крайне важно не забывать про масштаб графика. С виду идеальный диагональный график может на поверку таить в себе невязку в десятки метров.

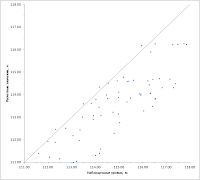
Два типичных графика: расчетные значения все дружно оказались выше или ниже наблюденных. В первом случае вы затопили, а во втором — пересушили модель. Если вы думаете, что я подскажу, как с этим бороться, то вы ошибаетесь. Увы, универсального рецепта не существует — все слишком сильно зависит от схематизации модели. Где-то надо поиграться с расходами на питающих границах, где-то менять фильтрационные параметры (характерно для многослойных толщ, в которых активно развито вертикальное перетекание — они бывают очень чувствительны к проницаемости разделяющих слоев), а где-то и вовсе придется пересматривать всю схематизацию. Ну, это если у вас вдруг настолько полные исходные данные, что ни фильтрационных свойств не изменишь, ни расходных характеристик, но это тоже больше из области ненаучной фантастики.

Самый неприятный вид диагонального графика, в худшем случае (первый кадр, очевидно) говорящий нам о том, что мы очень фиговые гидрогеологи и умудрились полностью перепутать направление движения подземных вод, а в более благоприятном (последний кадр) — о том, что нам не мешало бы увеличить градиенты потока. Но лично мне больше всего не нравится средний кадр, т.к. из него очевидно, что мы где-то накосячили, но непонятно — где. Из него видно, что градиент потока у нас получился недостаточный, но в каком направлении — не ясно.

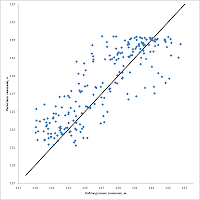
Еще один типичный вид диагонального графика — диагональ проходит через «облако» точек. Его особенность заключается в том, что в зависимости от характера исходных данных, он может как подтверждать достаточное качество решения обратной задачи, так и говорить об обратном. Удивительно, но объясняется просто. Если вы имеете дело с большим набором разновременных замеров уровня подземных вод (типичная ситуация при работе фондовыми данными), то совершенно невозможно «уложить все точки на диагональ» — просто потому, что для каждого замера характерны свои отличные от остальных граничные условия. Грубо говоря, часть замеров может быть сделано в зимнюю межень и характеризоваться уровнем заметно ниже среднегодичного, а часть - в весенний паводок, с уровнем выше среднегодичного. Пытаясь угодить и тем и этим вы получите либо страшно ошибочную модель, либо вообще ничего не добьетесь, только нервы потратите. Поэтому в данном случае обратную задачу можно считать решенной удовлетворительно, важно лишь следить за тем, чтоб разница между наблюденными и расчетными значениями не вылетала за амплитуду колебаний уровня подземных вод. А если делать все совсем по-уму, то надо на графике «меженные» и «паводковые» скважины рисовать разным цветом и следить, чтоб нужный цвет был с нужной стороны от диагонали.
Теперь совершенно очевидно, когда такой график будет говорить нам, что что-то мы напортачили в схематизации: когда вся масса замеров была проведена за относительно короткий промежуток времени, в течение которого не случалось резких изменений климатической обстановки. Кстати, из этого графика тоже понятно, что мы накосячили, но не совсем понятно — в чем.

Численным критерием качества решения обратной задачи традиционно является средний квадрат ошибки (Mean squared error, в PMWin он почему-то назван Variance), о котором я расскажу в следующий раз.

Subsurface and groundwater hydrology: Basic theory and application of computational methods

Коллега поделился замечательной книгой под авторством Tuomo Karvonen, профессора Helsinki University of Technology Department of Civil and Environmental Engineering: Subsurface and groundwater hydrology: Basic theory and application of computational methods. Книга представляет собой несколько упрощенную версию известной монографии Wolfgang Kinzelbach “Groundwater modelling”.
Раньше книга была выложена на личной странице автора, которая уже давно недоступна, да и сам автор пропал с экранов радаров. Думаю, я никому не наврежу, если выложу её в публичный доступ — не пропадать же такому добру.

How the Aquifer Works

Русская инструкция к MODFLOW

Вы не поверите, что я откопал! Я нашел частичный перевод инструкции к программе Processing Modflow 5-й версии. Я знал, что он существует — его делал мой научный руководитель в универе М.М. Кузнецов, но поскольку я достаточно свободно владею техническим английским, то мне он как-то не особо был нужен и я его не сохранил. Наткнулся я на него в профильном сообществе вКонтакте. В общем, кому надо, качайте: русскую инструкцию к Processing Modflow 5.3.
Версия конечно старая, но это во всяком случае лучшее из того, что есть. Кроме того, основные положения с тех пор практически не поменялись. Считайте это моим новогодним подарком читателям.

Кстати, о «верховодке»

Отчеты инженеров-геологов частенько грешат неправильным употреблением терминов «верховодка» и «грунтовые воды». Важно понимать, что это разные вещи.
«Верховодка» — локальный водоносный горизонт, невыдержанный по простиранию и времени существования, образующийся как правило в верхней части разреза в виде линз воды над относительно слабопроницаемыми грунтами (тоже часто залегающими в виде линз).
Грунтовый водоносный горизонт — первый от поверхности земли выдержанный по простиранию и времени существования водоносный горизонт.
Кстати, в чистом виде MODFLOW формирование «верховодки» считать не умеет. Т.е. если вам вдруг досталась задача по расчету осушения «верховодки», то либо придется менять инструмент, либо идти на «сделку с совестью» — считать её как полноценный водоносный горизонт, что приведет к заведомо завышенным расходам, а часто вообще невозможно в силу особенностей строения верхней части разреза.
Если же вода вскрыта не всеми скважинами, а водоупор не линзообразный, то это т.н. «горизонт спорадического распространения». Формально, каждая верховодка — горизонт спорадического распространения, но не каждый горизонт спорадического распространения — верховодка.